5. 다해상도
업샘플링upsampling : 해상도를 늘리는 영상 처리 연산
다운샘플링downampling : 해상도를 줄이는 영상 처리 연산
다양하게 변화된 상황(EX. 어떤 영상에서는 사람이 영상 전체에 나타나고, 다른 영상에서는 아주 작게 나타남)에 상관없이 물체를 안정적으로 찾아내고 인식하는 것은 컴퓨터 비전의 궁극적인 목표 중 하나이다.
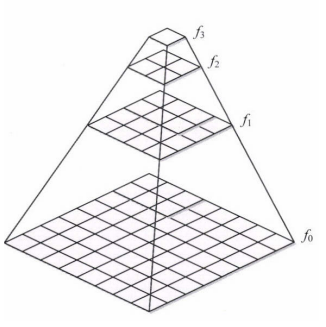
위의 이미지는 이러한 요구에 따라 고안된 기법인 영상 피라미드image pyramid이다.
피라미드는 해상도가 다른 여러장의 영상으로 구성된다. (f0 ~ f3)
이를 다중 해상도multi-resolution 영상이라고 부른다.
이 구조는 *거침과 세밀함 처리 방식에서 강점을 제공한다.
*거침과 세밀함coarse-to-fine 처리 방식 : 저 해상도의 거친 영상에서 물체의 대략적인 위치와 모양을 찾아낸 후, 고해상도의 세밀한 영상에서 정확한 위치와 모양을 결정하는 접근 방법.
피라미드는 샘플링 비율sampling rate인 r을 1/2로 설정하여 영상을 절반으로 다운샘플링하는 작업을 반복하여 만든다.
영상은 q단계까지 줄일 수 있는데, 원래 영상의 크기가 2ⁿ×2ⁿ이라면 q=n이다.
하지만 중간에 적당한 크기에서 멈추어 위가 평편한 피라미드를 사용한다.
(1/2로 계속해서 이미지를 다운샘플링하다보면 위가 뾰족한 1×1짜리 이미지가 남게된다. 필요한 영상은 화소 하나만 남은 이미지일리 없으므로, 중간에 멈추어 필요한 이미지를 사용한다는 이야기인 것 같다.)
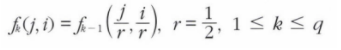
하지만 이 식은 단순하다는 장점이 있는 반면, 에일리어싱이 발생하는 심각한 문제를 안고 있다.
1/2로 다운샘플링하는 과정에서 짝수 좌표는 100% 참여하지만 홀수 좌표는 0% 참여하기 때문에 에일리어싱이 발생한다.
참여하지 못하는 화소에도 무시할 수 없는 정보가 들어있는 것이다.
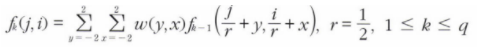
따라서 다운샘플링 이전에 스무딩을 적용하여, 스무딩-다운샘플링의 두 단계를 처리하여 다섯 화소의 가중치 곱의 합을 계산하여 목표로하는 좌표를 계산하게 된다.
이때, 가중치 역할을 하는 스무딩 커널 w 설계가 핵심이 된다.

위의 이미지는 하나의 행에 대해 h로 컨볼루션하여 다운샘플링하는 과정이다.
이 필터는 다섯 개의 값을 더하면 1이 되고, 모든 화소가 동일하게 0.5(50%)만큼 공헌한다는 성질도 만족한다. 그림에서 0.4만큼 공헌하는 점은 좌측, 우측 방향으로 0.05만큼씩 공헌하므로 총합이 0.5가 된다.
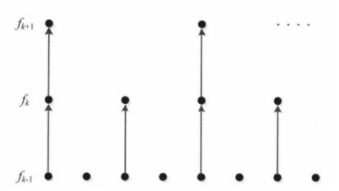
반면에 이전의 식은 어떤 점은 1만큼, 아니면 0만큼 공헌하게 되어 에일리어싱이 심각한다.
모든 점이 같은 정도의 공헌을 하도록 만드는 것은 안티 에일리어싱 효과가 있다.
현재까지는 1차원 필터를 살펴보았고, 2차원 필터로 확장하여 보면 아래와 같은 결과를 얻을 수 있다.

v와 h 필터를 곱하여 얻은 5×5 크기의 w 필터를 사용하는 것이다.
피라미드는 샘플링 비율 r을 1/2로 하여 영상을 반으로 줄여나간다. 하지만 r이 임의의 정수 또는 실수인 상황도 있다. 이런 경우는 보다 복잡한 업샘플링 or 다운샘플링 알고리즘을 사용해야 한다.
이때 에일리어싱 현상을 방지해야하는데, 영상 보간(EX. 최근접 이웃, 양선형, 양 3차 보간)으로 이 문제를 해결할 수 있다.
6. 모폴로지
수학적 모폴로지mathematical morphology : 영상의 나타난 물체의 모양을 분석하거나 원하는 형태로 바꾸는 작업을 하기 위해 사용하는 연산. 이진 영상에 작동하는 이진 모폴로지와 명암 영상에서 작동하는 명암 모폴로지로 나뉜다.
*모폴로지는 원래 생물학자들이 동물이나 식물이 보여주는 모양을 지칭하기 위해 사용하는 용어이다.
1. 이진 모폴로지
모폴로지는 구조요소structuring element를 사용하여 이진 영상에 있는 연결요소의 모양을 조작한다.
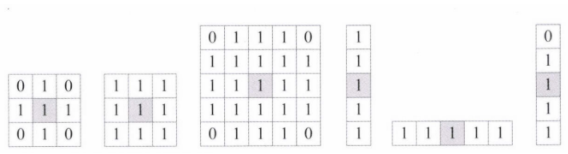
회색으로 표시된 화소 : 중앙
위의 그림과 같은 다양한 크기와 모양의 구조요소가 있다.
모폴로지에서 구조요소는 집합으로 표현하며, 값이 1인 요소만 집합에 속한다.
또한 구조요소는 비대칭일 수도 있다.
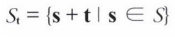
구조요소 S가 t만큼 이동한 새로운 집합은 위와 같이 정의된다.
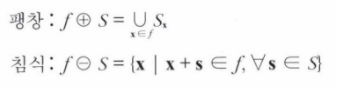
팽창dilation : f의 1인 화소에 구조요소를 씌우고 S의 1인 점과 겹치는 곳은 모두 1로 바꾼다 (합집합)
침식erosion : f의 어떤 화소에 구조요소를 씌운 곳에 구조요소의 1인 곳과 겹치는 곳이 모두 1인 경우만 그 화소를 1로 결정한다(교집합) 따라서 구조요소만큼 침식이 일어난다.
f는 1을 갖는 화소의 집합(구조요소)이다. 팽창에서의 x∈f는 영상 f에서 1을 갖는 화소 x를 의미한다.

열기opening : 침식된 영상에 팽창을 적용
닫기closing : 팽창된 영상에 침식을 적용
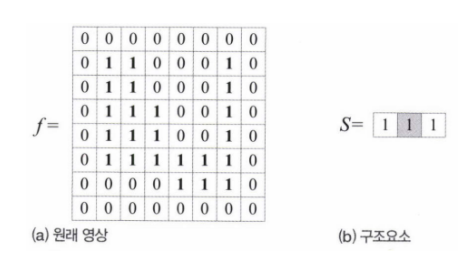
팽창/침식 연산을 사용할 때 구조요소가 수평방향이라면 수평 방향으로만 변화가 발생한다.
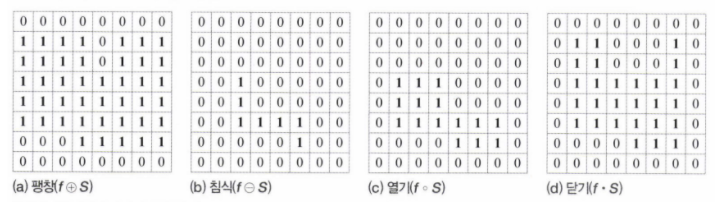
팽창 연산은 홈을 메우는 효과가 있으며, 구조요소의 모양과 크기에 따라 메우는 형태가 달라진다.
홈을 메우되 원래 크기를 유지하고 싶으면 침식을 추가로 적용하면 된다. (닫기 연산)
침식 연산은 구조요소보다 작은 크기의 돌출 부분을 깎는다. 침식된 영상에 팽창을 적용하면 깎여 없어진 부분을 제외하고 원래 크기로 복원된다. (열기 연산)
물체의 경계에 있는 홈 또는 돌출을 비롯해 물체의 내부에 꿇린 구멍에 대해서도 비슷한 효과가 있다. 팽창은 구멍을 메우며, 다시 침식을 적용하면 원래 크기로 돌아온다.
침식과 열기는 구멍에 대해서도 반대 작용을 한다.
2. 명암 모폴로지
명암 영상은 명암을 지표면부터의 높이로 간주하여 지형으로 해석할 수 있다.
명암 모폴로지는 이 지형에서 골짜기를 메우거나 봉우리를 깎는 효과를 제공해야 한다.

팽창은 지형을 솟구치게 해야하므로, 영상에 구조요소값을 더해준 후 최댓값을 취한다.
이때 구조요소의 좌표(y,x)를 빼주는데, 구조요소를 180° 회전하여 적용하는 것과 동일하다.
침식은 구조요소 값을 뺀 후 최솟값을 취함으로써 지형을 깎는 효과를 낸다.
영상의 경계에 구조요소를 씌우면 구조요소의 일부가 영상밖에 걸치게 되는데, 이런 경우를 처리하기 위해 영상 바깥은 모두 팽창에서 -∞, 침식에서는 ∞로 간주한다.

7. 컬러

RGB 모델은 가장 널리 이용되며, 크기가 1인 정육면체 공간 안에 모든 색이 있다.
컴퓨터에서는 이들을 정수 좌표로 표현하기 위해 [0, 1] 구간을 양자화quantization 하고, 길이가 1인 구간을 L개의 작은 구간으로 나누고 이들 구간에 0,1,2, ..., L-1의 정수 좌표값을 부여한다.
(c)의 경우엔 4^3으로 64개의 정사각형 블록이 생기지만, 실제 상황에서는 보통 L로 2^8=256을 사용한다.
총 표현 가능한 색상 수는 256^3이 되어 16,777,216개이다.
사람이 눈으로 구별할 수 있는 색을 모두 표현할 수 있다.
이때 한 화소를 표현하는 데 RGB 각각 1바이트 씩 3바이트가 필요하다.
'IT > Graphics' 카테고리의 다른 글
| 컴퓨터 비전 스터디 7주차 : 21.05.23 (0) | 2021.05.24 |
|---|---|
| 컴퓨터 비전 스터디 6주차 : 21.05.09 (0) | 2021.05.22 |
| 컴퓨터 비전 스터디 4주차 : 21.04.11 (0) | 2021.04.15 |
| 컴퓨터 비전 스터디 3주차 : 21.04.04 (0) | 2021.04.10 |
| 컴퓨터 비전 스터디 2주차 : 21.03.28 (0) | 2021.03.27 |




댓글